Describe
题目链接
经过数月的精心准备,Peer Brelstet,一个出了名的盗画者,准备开始他的下一个行动。艺术馆的结构,每条走廊要么分叉为两条走廊,要么通向一个展览室。Peer知道每个展室里藏画的数量,并且他精确测量了通过每条走廊的时间。由于经验老到,他拿下一幅画需要5秒的时间。你的任务是编一个程序,计算在警察赶来之前,他最多能偷到多少幅画。
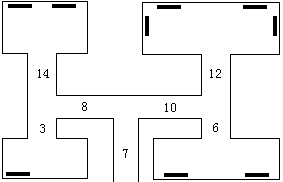
Solution
考虑$DP$。
设$f[i][j]$表示前$i$个还有$j$秒时间。
那么易得:
$$f[i][j]=max(f[ilson][k]+f[irson][time-t[x]-k])(0\leq k \leq time-t[x])$$
由于路是要走两次的(去一次回来一次)所以$t$数组要乘$2$。
注意小偷一定要在警察来之前跑走,所以$s$要减一。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| #include<bits/stdc++.h>
using namespace std;
int s,t[1010],a[1010],f[1010][1010];
inline void init(int x){
scanf("%d%d",&t[x],&a[x]);
t[x]*=2;
if(!a[x]) init(x<<1),init(x<<11);
}
inline int dfs(int x,int tim){
if(!tim) return 0;
if(f[x][tim]) return f[x][tim];
if(a[x]) return f[x][tim]=min(a[x],(tim-t[x])/5);
for(int i=0;i<=tim-t[x];i++)
f[x][tim]=max(f[x][tim],dfs(x<<1,i)+dfs(x<<11,tim-t[x]-i));
return f[x][tim];
}
int main(){
scanf("%d",&s);--s;
init(1);
printf("%d\n",dfs(1,s));
}
|
