1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
|
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cctype>
#include<cerrno>
#include<cfloat>
#include<ciso646>
#include<climits>
#include<clocale>
#include<cmath>
#include<csetjmp>
#include<csignal>
#include<cstdarg>
#include<cstddef>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<ctime>
#define MAXN 510
#define eps 1e-8
#define MAXM 5000010
using namespace std;
inline int read(){
int res=0,f=1;char ch=getchar();
while(ch<'0'ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(int x){
if(x<0) putchar('-'),x=-x;
if(x<10) putchar(x+'0');
else{
write(x/10);
putchar(x%10+'0');
}
}
double a[MAXN][MAXN];
void Gauss(int n){
for(int i=0;i<n;i++){
int Cho=i;
for(int j=i;j<n;j++){
if(fabs(a[j][i]-a[Cho][i])<=eps) Cho=j;
}
for(int j=0;j<=n;j++){
swap(a[i][j],a[Cho][j]);
}
if(fabs(a[i][i])<=eps){
puts("No Solution\n");
exit(0);
}
for(int j=i+1;j<=n;j++) a[i][j]/=a[i][i];
for(int j=0;j<n;j++){
if(i!=j) for(int k=i+1;k<=n;k++) a[j][k]-=a[j][i]*a[i][k];
}
}
}
int n,m;
int fir[MAXM],nxt[MAXM],w[MAXM],son[MAXM],tot;
int deg[MAXN],u[MAXM],v[MAXM];
double f[MAXM],ans;
struct node{
double g;
int id;
}K[MAXM];
void add(int x,int y,int z){
++tot;
nxt[tot]=fir[x];
son[tot]=y;
w[tot]=z;
fir[x]=tot;
}
bool cmp(node qx,node qy){
return qx.g>qy.g;
}
int main(){
n=read();m=read();
for(int i=1;i<=m;i++){
u[i]=read(),v[i]=read();
add(u[i],v[i],0);
add(v[i],u[i],0);
deg[u[i]]++;deg[v[i]]++;
}
for(int i=1;i<n;i++){
a[i-1][i-1]=1.0;
for(int to,j=fir[i];j;j=nxt[j]){
to=son[j];
if(to!=n) a[i-1][to-1]=-1.0/(double)deg[to];
}
if(i==1) a[i-1][n-1]=1.0;
}
Gauss(n-1);
for(int i=1;i<=n;i++) f[i]=a[i-1][n-1];
for(int i=1;i<=m;i++){
if(u[i]!=n) K[i].g+=(f[u[i]]/(double)deg[u[i]]);
if(v[i]!=n) K[i].g+=(f[v[i]]/(double)deg[v[i]]);
K[i].id=m;
}
sort(K+1,K+m+1,cmp);
for(int i=1;i<=m;i++) ans+=i*K[i].g;
printf("%.3lf\n",ans);
return 0;
}
|
将上面的方程转为下面的增广矩阵 
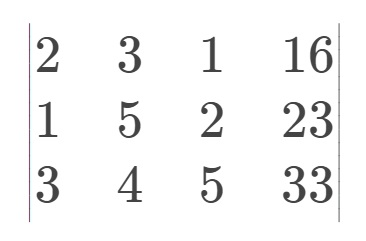接下来进行高斯消元。 首先找到一个第一列的数不为0的行（一般找第一列的数最大的行）（如果都为0就跳过当前步） 然后用它的第一列的数将下面行当前列的值化为0，变换过的初等矩阵与原矩阵等价，化为方程后依然成立 本矩阵第一列的数最大的为第三行就把第三行与第一行交换 
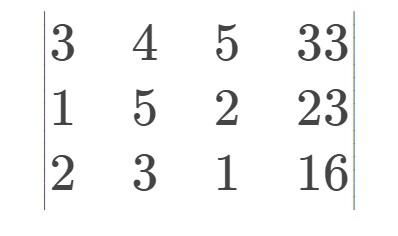然后下面行的当前列消去，如图 
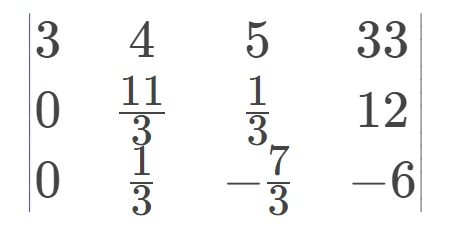除了最后一列外，每一列都如此，最后得到上三角矩阵如图 
这样我们就可以轻松求出$x1,x2,x3$了。 回归到这道题 我们设$deg_i$表示第$i$个点的度数，$f_i$表示第$i$个点期望经过次数： 
由于当小$Z$到达$n$点时就停止游走了，因此不能考虑$n$点。接下来对$n−1$个$f_i$进行高斯消元求解。 设$g_i$表示第$i$条边期望经过次数： $g_{i}=\frac{f_{u}}{d_{u}}+\frac{f_{v}}{d_{v}} \quad E_{i}=(u, v), u \neq n, v \neq n$ 最后排序，贪心，因为要求期望值最小，那么就把最大的$g_i$编号标至最小，以此类推。