10238. 「一本通 6.6 练习 9」网格
题意
某城市的街道呈网格状,左下角坐标为 $A(0, 0)$,右上角坐标为 $B(n, m)$,其中 $n \ge m$。现在从 $A(0, 0)$ 点出发,只能沿着街道向正右方或者正上方行走,且不能经过图示中直线左上方的点,即任何途径的点 $(x, y)$ 都要满足 $x\ge y$,请问在这些前提下,到达 $B(n, m)$ 有多少种走法。 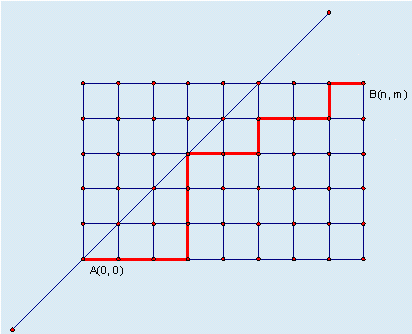
思路
很容易就可以想到答案是$C(n+m,m)-C(n+m,m-1)$ 当然,你打C++高精也可以。。。 python更省力啊。。。
1 | n,m=map(int,input().split())//读入一行内两个整数 |